Reaction Mechanism and Reaction Dynamics

III) Reaction Mechanism and Reaction Dynamics

A) Development and Application of URVA: Unified Reaction Valley Approach

1. The Unified Reaction Valley Method for Studying Reaction Mechanism and Reaction Dynamics

(Professor Elfi Kraka, Professor Dieter Cremer)

The standard procedure to investigate the mechanism of a chemical reaction is to locate the stationary points of reactants, products, and transition state (TS) on the potential energy surface (PES) and, then, to relate the differences observed for energies, geometries and other molecular properties to changes in the electronic structure of the reaction complex along the reaction path. The analysis of the three stationary points along the reaction path provides valuable, but rather incomplete information on the reaction mechanism.

Based on our previous work on the reaction path hamiltonian, we have developed in the last year a new and more complete approach to the description of reaction mechanism. We have coined the name "Unified Reaction Valley Approach (URVA)" since the analysis is based on the exploration of the reaction valley embedding the reaction path in (3K-6)-dimensional space (K: number of atoms of the reaction complex). This is done in the harmonic approximation by calculating at each investigated path point the 3K-7 generalized normal modes orthogonal to the path as is required by the reaction path hamiltonian (RPH) of Miller, Handy, and Adams (J. Chem. Phys. 1980, 72, 99). Couplings between vibrational modes and the translational mode along the reaction path as well as among the vibrational modes themselves are used to describe energy transfer and energy dissipation, rate enhancement, and rate decrease as well as substituent and environmental effects on the reaction.

Much work has been done with the RPH to explore the behavior of reaction systems with 3 or 4 atoms. However, our approach differs from other work in the way that it is technically (in terms of the computer programs written by us) more advanced and that it is based on local vibrational modes rather than normal modes commonly used to describe the reaction mechanism. Normal modes are relatively easy to interpret as long as rather small reaction systems are investigated, however for larger reaction systems this becomes almost impossible. The normal modes represent delocalized modes, which are far from chemical thinking since the average chemist prefers to discuss molecules in terms of localized properties such as bond length, bond strength, etc. Therefore, it is the question how delocalized normal modes can be transformed to localized modes, which are associated with bonds or other chemically relevant subunits of a molecule.

We have developed a method that transforms calculated vibrational modes to localized adiabatic vibrational modes so that the RPH analysis can be performed in a way that provides direct chemical insight into the reaction. For the local adiabatic modes, we determine frequencies and force constants characteristic of the chemical bonds or other chemically interesting subunits of a molecule. Utilizing the local modes, we can directly determine which part of a reaction system is responsible or predominately involved in a special mechanistic effect. We can investigate each step of the reaction in detail, which gives us an extremely powerful tool for analyzing chemical reactions. The analysis comprises the following steps:

Calculation of the energy profile along the reaction path described in terms of the mass-weighted reaction coordinate s.
Calculation of all geometrical changes as a function of s.
Analysis of the reaction path direction in terms of internal coordinates using the adiabatic mode concept.
Calculation of the energy gradient as a function of I, analyzing it in terms of forces associated with internal coordinates and identifying regions of repulsive and attractive interatomic forces.
Calculation of the normal mode frequencies of the reaction complex as a function of s.
Calculation of adiabatic forces and adiabatic frequencies of the reaction complex along the reaction path.
Analysis of all normal modes in terms of adiabatic modes.
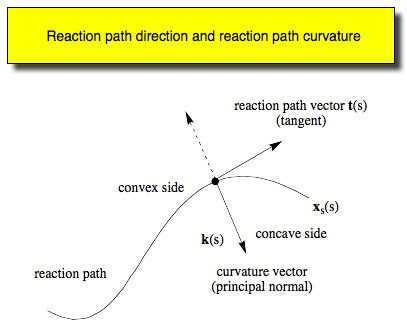
Calculation of the reaction path curvature and the curvature coupling coefficients describing the dynamic coupling between the motion along the reaction path and the 3K-7 normal modes orthogonal to the reaction path.
Decomposition of the reaction path curvature in terms of adiabatic mode-curvature coupling coefficients.
Analysis of the mode-mode coupling pattern.
Analysis of those vibrational modes that are converted into (generated from) translational/rotational modes.
Analysis of changes in the electron density distribution along the reaction path with the help of electron difference densities, the Laplacian of the electron density, and the virial partitioning method.
Determination of catastrophe points in electron density space and relating them to changes in the structure of the reacting system as well as to changes in the reaction path curvature.
Calculation of rate constants with the help of variational transition state theory.
Investigation of tunneling effects, isotope effects, etc. if appropriate.

The analysis 1) - 15) constitutes URVA and represents a unique way of investigating chemical reactions since it combines the traditional approach based on an investigation of the stationary points of the PES with the concepts of the reaction valley and the RPH, the analysis of the electron density distribution, catastrophe theory and variational transition state theory. Steps 3, 4, 8, 9, and 12 provide a detailed insight into the reaction mechanism. Steps 8 and 10 will lead to a description of mode specific rate enhancement, energy transfer, and energy dissipation along the reaction path.

Utilizing URVA, we have investigated a number of chemical reactions:

a) Investigation of pericyclic reactions: We investigated both concerted and non-concerted pericyclic reactions (Diels-Alder reaction, [2+2] cycloadditions, etc.). The investigations reveal that bond breaking and bond forming can take place before and after the transition state and is always coupled with a series of geometrical changes that follow each other in a domino effect. Investigation of the reaction path curvature has led us to assume the following mechanistically important relationships:

The number of peaks of the curvature of the reaction path corresponds to the number of bond cleaving and bond forming processes.
The sequence of the curvature peaks corresponds to the order in which the bonds are broken or formed.
The height of the curvature peaks is related to the magnitude of the energy changes involved in a particular process.

b) Investigation of reactions in solution: It is a challenging goal to apply the URVA analysis for reactions that take place in solution. We used a continuum model for this purpose.

For further reference, see:

105
Characterization of Molecular Potential Energy Surfaces: Critical Points, Reaction Paths and Reaction Valleys, E. Kraka, T. H. Dunning, Jr., in "Advances in Molecular Electronic Structure Theory: The Calculation and Characterization of Molecular Potential Energy Surfaces, T.H. Dunning. Jr., Edt, JAI Press, Inc., Greenwich, 1990, p.129.
177
Unified Reaction Valley Approach: Mechanism of the Reaction CH₃ + H₂ → CH₄ + H, Z. Konkoli, E. Kraka, and D. Cremer, J. Phys. Chem. A, 101, 1742 (1997).
179
Diabatic Ordering of Vibrational Normal Modes in Reaction Valley Studies, Z. Konkoli, D. Cremer, and, E. Kraka, J. Comp. Chem., 18, 1282 (1997).

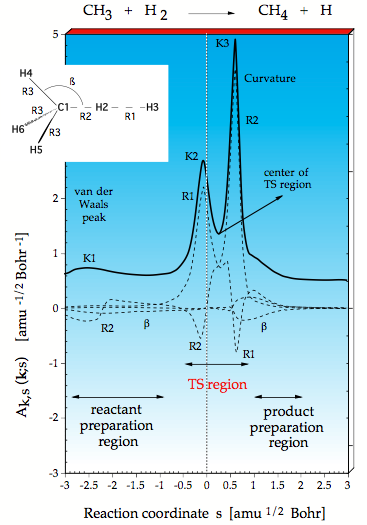
Figure 1. Decomposition of the reaction path curvature k(s) (thick solid line) in terms of adiabatic mode-curvature coupling amplitudes A_n,s(s) (dashed lines). The curvature k(s) has been shifted by 0.5 units to more positive values to facilitate the distinction between k(s) and A_n,s(s). The position of the transition state corresponds to s = 0 amu ^½ bohr and is indicated by a vertical line.

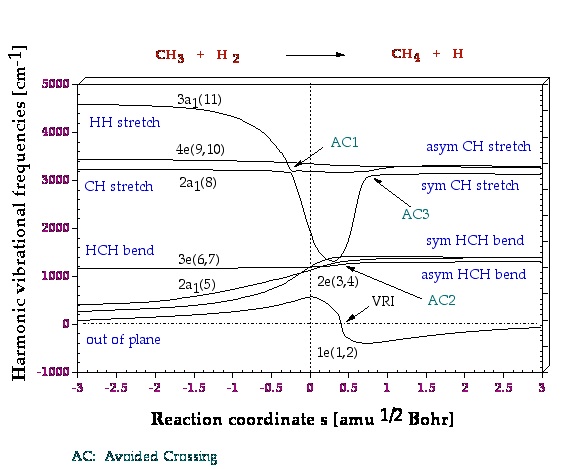
Figure 2. Adiabatic representation of normal mode frequencies w_m(s). Symmetry symbols and numbering of no brmal modes are given according to the order of normal modes calculated for the reactants. The position of the transition state corresponds to s = 0 amu^0.5 bohr and is indicated by a dashed vertical line. The value w((1e)(s) = 0 corresponds to the valley ridge inflection point VRI at s = 0.4 amu0.5 bohr. Imaginary 1e frequencies calculated for s > 0.4 amu0.5 bohr are given as negative numbers. The pointsAC1, AC2, and AC3 correspond to avoided crossings

Using URVA the reaction CH₃ + H₂ → CH₄ + H was investigated. There are two regions of strong curvature of the reaction path, namely at K2 where the HH bond starts to break and at K3 where the CH bond is formed. These are the points, at which the translational motion along the reaction path strongly couples with vibrational modes so that an energy transfer becomes in principle possible.

Knowing these couplings one can give a laser spectroscopist valuable information for mode pumping in connection with mode selective rate enhancement.

We decompose the scalar curvature into contributions from localized (adiabatic) vibrational modes associated with the internal coordinates used to describe the reaction complex. In this way we find that the HH stretching motion is associated with K2, the CH stretching motion with K3, however the CH mode contributes also to K2 and the HH mode to K3 as can be seen by the negative R2 and R1 components in Figure 1. They are negative because the corresponding internal coordinate motion resists a curving of the path and the electronic structure changes associated with it. The decomposition of the curvature into adiabatic modes reveals that HH bond rupture and CH bond formation start at the same time and terminate at the same time. These chemical processes are indicated in such a diagram by large curvature peaks, which in turn define the TS region (region of bond cleavage and bond formation). One can define the center of the TS region (Figure 1) and see that with regard to this center the energy TS is moved into the entrance channel (early TS), which is in line with the Hammond postulate since the reaction is exothermic. – There is a smaller curvature peak K1 located in the entrance channel, which indicates the point where the planar methyl radical starts to become pyramidal due to the van der Waals (vdW) interactions with the H2 molecule. Hence, we can detect the region of vdW interactions, even when these do not lead to a vdW complex. K1 defines the point where the reaction starts. After the vdW region, there is a preparation region where the reactants prepare for the reaction taking place in the TS region. The product preparation region follows the TS region but in this diagram it is just a shoulder and there is no vdW peak in the curvature diagram. This can easily be understood considering that a H atom has only a small polarizing power. Therefore, it has to get close to CH₄ to polarize the CH bond, which is rapidly done so that CH bond breakage follows immediately.

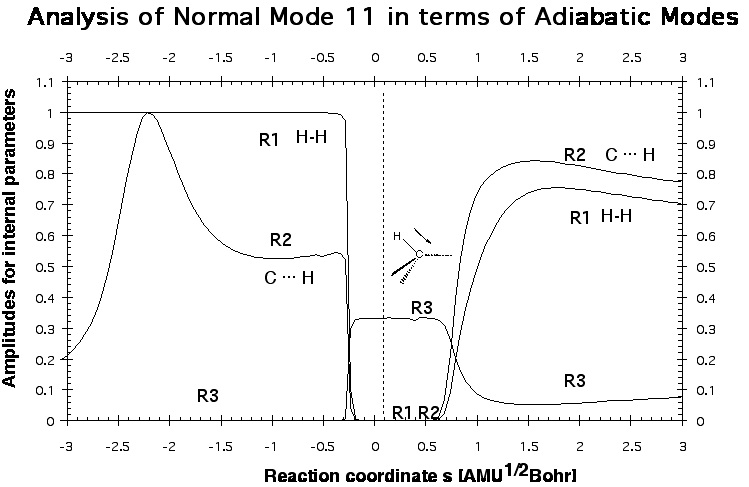
Figure 3. A decomposition into adiabatic (localized) modes is shown for mode 11, which is first the HH stretching mode. At the first avoided crossing, AC1 (Figure 2), it becomes a CH stretching mode of a spectator bond, and at the second avoided crossing, AC3 (Figure 2), it changes to the stretching mode of the newly formed CH bond.

One gets a very detailed description of the mechanism, which is supported by the analysis of other properties of the reaction complex along the reaction path. One learns that mechanistically the energy TS is not so important because the chemical processes start before and end considerably after the TS. Mode 11 in Figure 2 has the strongest dependence on the reaction path and therefore one wants to know which internal coordinate modes are affected by mode 11.