III) Reaction Mechanism and Reaction Dynamics
A) Development and Application of URVA: Unified Reaction Valley Approach
2. Diabatic Mode Ordering (DMO)
A requirement for the calculation of the curvature and Coriolis couplings within URVA is that the normal modes are correctly ordered when going from one point of the reaction path to the next point. Since the normal modes may interact along the reaction path, the ordering of the normal modes is nontrivial, but very important. For most molecules, this ordering can be carried out with the help of symmetry, however for molecules without any symmetry such a procedure cannot be used. There are also situations, characterized by an artificial distortion of the symmetry of the reaction complex due to a large step size along the reaction path, in which a symmetry-based ordering becomes impossible. Konkoli, Kraka, and Cremer have developed the diabatic mode ordering (DMO), which is independent of symmetry. It has been successfully applied to chemical reactions and reaction complexes with 50 and more normal modes.
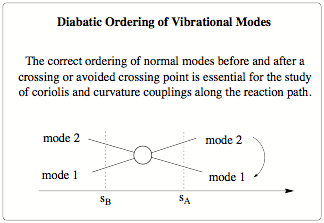
Scheme 1: Diabatic ordering of two crossing modes
There are two major factors causing changes in the normal modes along the reaction path. The first one is a global rotation of the normal modes induced by changes in direction of the reaction path. Any change in the direction of the reaction path will lead to a rotation of the (3N-7) dimensional space spanned by the normal modes with regard to the previous step. Going from step A to step B the normal modes at step B will be a slightly rotated mirror image of the modes at step A, where the degree of rotation will be determined by the step size between A and B. The second cause is the interaction or mixing of different normal modes along the reaction path. As the reaction complex moves along the reaction path the contour of the reaction valley changes and so does the force constant matrix. Energy will be transferred between the normal modes and as a result allowed and avoided crossings may take place. The avoided crossings will lead to a character change between the involved modes, and thus a significant change in the normal modes. - In the DMO algorithm the ordering of the normal modes is based on maximum overlap criteria. For each new point on the reaction path, the calculated normal modes are ordered and rotated according to the normal modes in the previous step so that the overlap between them is maximized. The ordering and rotation takes care of the global rotations of the path and the individual changes of the modes. Special care is taken for degenerate modes to ensure correct ordering between the steps.
4. Do barrierless Reactions possess a Mechanism?
For exothermic reactions without a classical barrier (a TS may exist nevertheless because of centrifugal effects), a well-defined steepest descent path leading from reactants to products does no longer exist. The reaction complex can follow many paths that are collected in the reaction valley leading down to the product minimum. For dynamics calculations this may not pose an unsolvable problem as was recently demonstrated by Bofill and co-workers, however for the mechanistic investigation where unbiased information is only provided by the minimum energy path, this is more difficult. Currently, we work on an uphill path-following algorithm based on gradient extremals and Newton trajectories. Gradient extremals connect stationary points on a molecular PES and are locally characterized by requiring that the molecular gradient is an eigenvector of the mass-weighted molecular Hessian at each point on the line. Starting from the minimum (position of the products) one can define the "valley floor gradient extremal", which corresponds to the smallest (absolute) eigenvalue of the Hessian. Such a valley floor path fulfills the condition that the energy increases along all directions perpendicular to the direction of the valley floor line. Also, the curvature of the energy surface along the direction of the valley is less than the curvature along any other direction. We will use a projector technique where the projector is built by the tangent of the valley floor line. This part of the project will be done in collaboration with Professor W. Quapp, University of Leipzig, Germany. Objective of the project is to find a path in the case of a barrierless reaction, which leads from the valley minimum to the high-lying energy plateau, which is the location of the dissociation products. Once this path has been determined URVA can be used and the mechanism of the barrierless reaction analyzed.
In basic chemistry courses, it is often argued that chemical reactions follow a least-motion path (least changes in electronic structure and geometry of the reaction partners). In recent research, we found that the concerted addition of vinylidene to acetylene, which according to Woodward-Hoffmann is symmetry-allowed in the nonlinear (!) s,s approach mode of the reaction partners, follows a complicated reaction mechanism even though the reaction proceeds without an activation enthalpy directly to the product. At larger distance between the reaction partners, the reaction complex is planar; then, vinylidene approaches acetylene and enforces a trans rather than a cis distortion of acetylene. Next, vinylidene rotates out of the plane to form an intermediate structure, which reminds of allenyl carbene. A further approach of vinylidene to acetylene leads to a cis deformation of acetylene and a back-rotation of the CH2 group in vinylidene so that again a planar reaction complex is obtained; finally, the product methylenecyclopropene is formed (see Figure 1).
Hence, the reacting molecules dance around each other where the choreography is written by electronic structure requirements. An intermediate structure can be identified as allenyl carbene even though the energy profile along the reaction path does not show any local minimum. We have coined the term hidden intermediates for these structures, which is justified in view of experimental observations made parallel to our investigation: Addition of the perfluorinated vinylidene to difluoroacetylene does lead to an intermediate perfluorinated allenyl carbene, which was detected by low temperature infrared spectroscopy (Chem. Eur. J. 4, 2353, 1998).
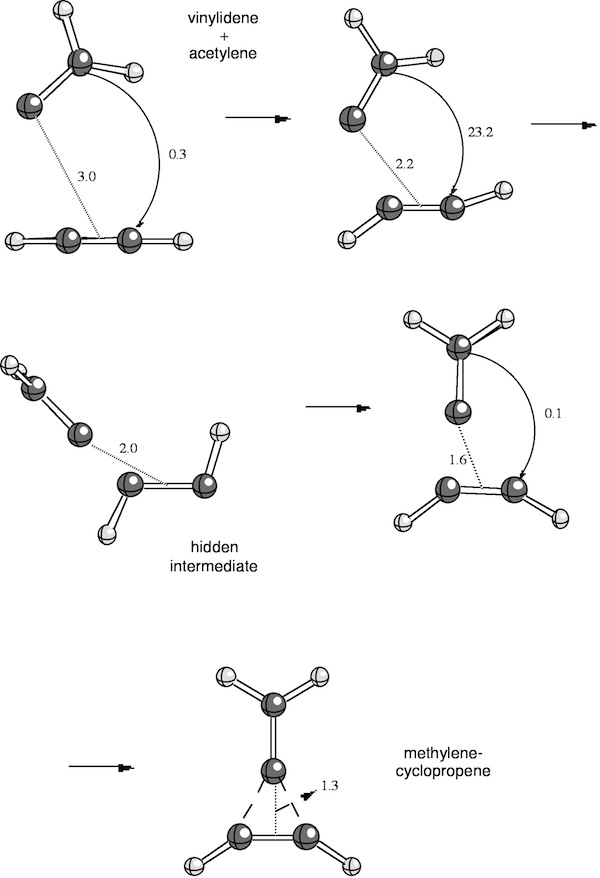
Figure 1. Chelotropic addition of vinylidene to acetylene.
5. Search for Hidden Intermediates
(Project leaders: Dr. E. Kraka and Dr. D. Cremer)
A fundamental goal in chemistry is to control chemical reactions. This goal can only be achieved by advanced understanding of the reaction mechanism and its sensitivity to environmental influences (temperature, pressure, solvent, etc.). Kraka and Cremer have discovered the “hidden intermediates” which do not exist in a chemical reaction, which however can be allocated on the potential energy surface of a reactive system. If analyzed with the methods of Kraka and Cremer, it is possible to predict those conditions that transform a hidden intermediate into a real intermediate and by this lead to a change in the reaction mechanism. – For the reaction system ethene-HX (X =O Cl, Br) the Kraka-Cremer methods are applied and results are compared with the stressian description of the reaction complex as worked out by Tachibana. In this way, the project aims at obtaining a more general description of hidden intermediates and their role in reaction mechanism.
According to our present theory, hidden intermediates can exist in connection with concerted but symmetry-forbidden reactions or in reactions, for which symmetry or other electronic factors force the reaction complex to follow a non-least motion path. We will search for hidden intermediates utilizing the repertoire of methods worked out by the members of PCTC, in particular the unified reaction valley approach, based on the reaction path hamiltonian (Miller, Handy, and Adams, J. Chem. Phys. 1980, 72, 99) and the adiabatic mode concept (D. Cremer, Z. Konkoli, Int. J. Quant. Chem., 67, 1, 1998). In URVA calculations, reaction path direction and curvature as well as energy, geometry, forces, vibrational modes, electron density, and many other properties of the reaction complex will be calculated, which provide a very detailed description of the reaction mechanism and by this the description of hidden intermediates. (see A.1)
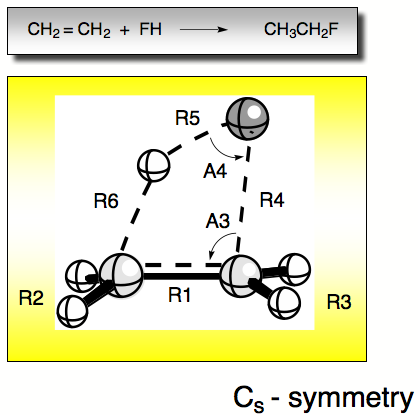
Figure 1. Internal coordiantes of the reaction complex FH + ethene.
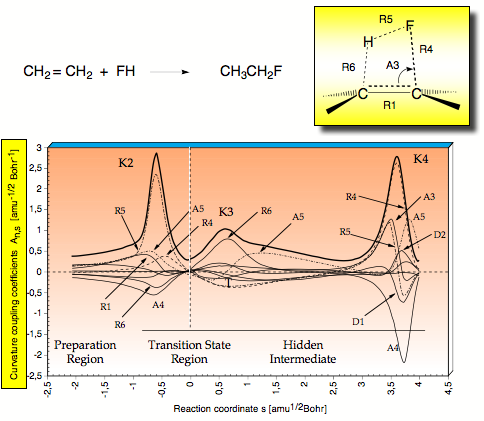
Figure 2. Decomposition of the scalar reaction path curvature k(s) (thick solid line) in terms of adiabatic mode-curvature coupling amplitudes An,s(s) (thin and dashed lines). The curve k(s) is shifted by 0.1 unit to more positive values to facilitate the distinction between k(s) and An,s(s). Curvature peaks and reaction regions are indicated. For a definition of parameters, compare with Scheme 2. The position of the TS corresponds to s = 0 amu1/2 Bohr and is indicated by a dashed vertical line.
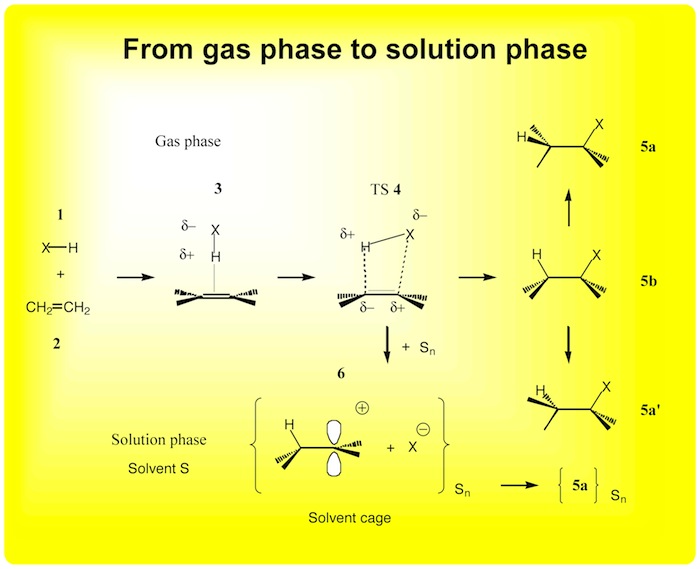
Figure 3. Mechanism of the cycloaddition HX + ethene in the gas and the solution phases in dependence of X.
6. Mechanism of the Bergman reaction
It is generally assumed that the Bergman reaction of an enediyne is a symmetry-allowed disrotatory electrocylic reaction. Various authors have raised criticism with regard to this interpretation. According to these authors the reaction is hindered in the entrance channel by a symmetry-forbidden [2+2]-interaction between the terminal alkinyl groups, which leads to the relative high reaction barrier of the Bergman cyclization (DE = 30.1 kcal/mol). According to this hypothesis, a lowering of the reaction barrier can be achieved by any structural perturbation that decreases four-electron repulsion in the TS, for example by placing an acceptor substituent in the proximity of the acetylenic in-plane p-orbitals. - Since we have worked out the methods to investigate such a claim in detail, we will apply our unified reaction valley approach to the problem. This approach will clarify the mechanism directly via reaction path direction and curvature diagram (decomposed into adiabatic modes). The analysis will reveal a) whether the mechanism is first characterized by a [2+2]-step and changes later to a ring closure reaction; b) how the reaction barrier can be manipulated electronically, and c) how environmental effects will change the mechanism and the barrier. We plan to carry out this analysis with methods ranging from BS-UDFT to REKS-DFT and CAS-DFT.
7. The Reaction Mechanism of Ketene Cycloadditions
The thermal [2+2]-cycloaddition of keteneophiles (ethylene, formaldehyde, formimine) and ketenes is forbidden in the p2s+p2a mode, but symmetry-allowed in the stereochemically more difficult p2s+p2a mode. There is a controversy in the literature whether these reactions proceed via a concerted route or via a two-step mechanism. For example, in the case of the ketene-formimine addition both a concerted and a non-concerted mechanism are discussed. Our URVA analysis will provide a detailed analysis of the electronic and dynamic features dominating the reaction mechanism. This project will be carried out with Professor D. Birney (Dept. of Chemistry and Biochemistry, Texas Tech University), who will carry out kinetic and spectroscopic studies to the problem. In this way, the reliability and applicability of the Woodward-Hoffmann rules will be tested in an extreme case.
