IX) Vibrational Spectrocopy
1. Description of Vibrational Spectra in terms of Adiabatic Internal Modes
(Professor Elfi Kraka, Professor Dieter Cremer)
Vibrational spectroscopy is a frequently used tool to identify and characterize a molecule with the help of its vibrational modes. Depending on its geometry, conformation, and electronic structure, each molecule has typical vibrational spectra that are measured with the help of infrared or Raman spectroscopy. For example, an infrared band at 1700 cm-1 is typical of a carbonyl stretching frequency or one at 700 to 800 cm-1 of a CCl bond stretching frequency. In this way, one can draw conclusions from the measured vibrational spectra with regard to the structure of a compound.
The amount of information contained in a measured vibrational spectrum is exploited to some, but not to its full extent. For example, vibrational spectra are never used to characterize all bonds of the molecule and to describe its electronic structure and charge distribution in detail. Of course, aspects of such investigations can be found off and on in the literature, however, both quantum chemists and spectroscopists fail to use vibrational spectra on a routine basis as a source of information on bond properties, bond-bond interactions, bond delocalization or other electronic features. Therefore, it is correct to say that the information contained in the vibrational spectra of a molecule is not fully utilized. This has to do with the fact that the analysis of vibrational spectra is always carried out in a way that is far from chemical thinking. The basic instrument in this respect is the normal mode analysis (NMA), which describes the displacements of the atomic nuclei during a molecular vibration in terms of delocalized normal modes.
We worked out a new way of analyzing calculated vibrational spectra in terms of internal vibrational modes associated with the internal coordinates used to describe geometry and conformation of a molecule. The internal modes are determined by solving the Euler-Lagrange equations for molecular fragments fn being characterized by internal coordinates qn. An internal mode is localized in a molecular fragment by describing the rest of the molecule as a collection of massless points that just define molecular geometry. Alternatively, one can consider the new fragment modes as motions that are obtained after relaxing all parts of the vibrating molecule but the fragment under consideration. Because of this property, the internal modes are called adiabatic internal modes (AIMs). Once the AIM vectors are known, adiabatic force constants ka, adiabatic frequencies wa, and adiabatic masses ma (corresponding to 1/Gnn of Wilson's G matrix) are determined. The AIMs are independent of the set of internal coordinates used to describe molecular geometry, comply with the symmetry of the molecule, and lead to a clear separation of mass and electronic effects in the vibrational modes of the molecule.
The AIMs are perfectly suited to analyze the vibrational spectra of a molecule in terms of internal coordinate modes, to correlate the vibrational spectra of different molecules, and to extract chemically useful information directly from vibrational spectra. We showed that AIM stretching frequencies and force constants correlate with the corresponding bond lengths and that this can be used to extend Badger's rule from diatomic to polyatomic molecules. The intensities of adiabatic stretching modes lead to effective atomic charges and bond dipole moments. Generalized AIMs are defined for reacting molecules located somewhere along the reaction path. They are used to analyze the direction and curvature of the reaction path and, by this, to obtain a better insight into reaction mechanism and reaction dynamics.
For further reference, see:
- 181A New Way of Analyzing Vibrational Spectra I. Derivation of Adiabatic Internal Modes, Z. Konkoli and D. Cremer, Int. J. Quant. Chem., 67, 1 (1998).
- 182A New Way of Analyzing Vibrational Spectra II. Comparison of Internal Mode Frequencies, Z. Konkoli, J. A. Larsson and D. Cremer, Int. J. Quant. Chem., 67, 11 (1998).
- 183A New Way of Analyzing Vibrational Spectra III. Characterization of Normal Vibrational Modes in Terms of Internal Vibrational Modes, Z. Konkoli and D. Cremer, Int. J. Quant. Chem., 67, 29 (1998).
- 184A New Way of Analyzing Vibrational Spectra IV. Application and Testing of Adiabatic Mode Vectors within the Concept of the Characterization of Normal Modes, Z. Konkoli, J. A. Larsson and D. Cremer, Int. J. Quant. Chem., 67, 41 (1998).
- 187New Developments in the Analysis of Vibrational Spectra: On the Use of Adiabatic Internal Vibrational Modes, D. Cremer, J. A. Larsson, and E. Kraka, Theoretical and Computational Chemistry, Volume 5, Theoretical Organic Chemistry, C. Parkanyi, Edt., Elsevier, Amsterdam, 1998, p.259.
Fig. 1: Adiabatic CC stretching mode of bond C4C10 in naphthalene.
The normal vibrational modes of the naphthalene molecule embed (in a coded form) information about each CC bond in the molecule. However, the modes measured are delocalized modes, which involve the whole carbon frame of naphthalene. One can decouple a single CC stretching mode by solving the Euler-Lagrange equations of vibrational spectroscopy and setting all atomic masses of the molecule to zero with the exception of the masses of C4 and C10 (see Figure 1). This can be done by a constrained minimization using Lagrange multipliers for any pair (triple, multiple) of atoms in a molecule so that, e.g., all individual CC stretching modes of naphthalene are obtained.
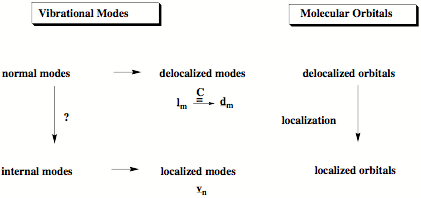
Figure 1. Chemists prefer to describe chemical bonding with localized orbitals. In the same way it is easier for chemists to understand the vibrational modes of a molecule in terms of localized internal modes associated with the internal coordinates of the molecule (we call them adiabatic modes) rather than delocalized normal modes. We solved the problem (question mark above) how to derive these localized vibrational modes from normal modes.
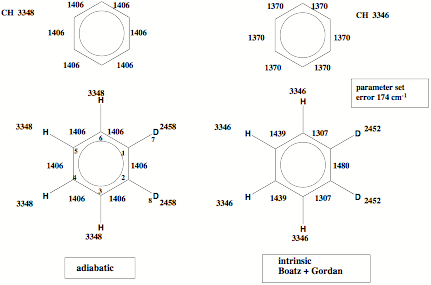
Figure 2. The adiabatic vibrational modes are typical of the bonding situation rather than the isotope mass as is the case for the intrinsic vibrational modes of Boatz and Gordon.
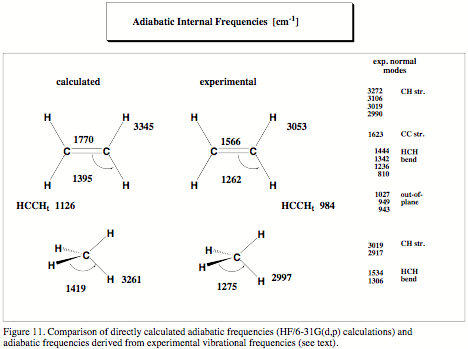
2. Vibrational Spectroscopy as a Primary Source of Information on Chemical Bonding
(Professor Elfi Kraka, Professor Dieter Cremer)
Since the early work of Badger in the mid 30s it has been a long dream of chemists to obtain information on chemical bonding from vibrational spectroscopy. Badger could relate bond strength to bond stretching force constant and stretching frequency, however his relationships ("Badger rule") were valid only for diatomic molecules. A generalization of the Badger rule to polyatomic molecules was not possible since in a polyatomic molecule vibrational modes are delocalized due to coupling effects. A stretching frequency or stretching force constant typical of a special bond is difficult to determine. Because of this, there was so far only one genuine successor of Badger, who was able to extend Badger's work to polyatomic molecules: In the 70s, McKean (Chem. Soc. Rev. 1978, 7, 399) managed to determine isolated CH stretching frequencies and force constants characteristic of the CH bond strength by synthesizing many D-isotopomers of hydrocarbons and, then, measuring their infrared spectra. Since then, McKean's work remained a highlight in the investigation of bond strength because its extension to other than CH bonds turned out to be impractical.
Goal of our project is to make Badger's and McKean's work generally applicable by utilizing a new definition of localized vibrational modes that provides for the first time for each bond of a polyatomic molecule a characteristic stretching frequency and force constant, which is not contaminated by any coupling effects. We have already demonstrated that the McKean relationship between CH stretching frequencies and CH bond lengths is verified for the adiabatic internal mode (AIM) frequencies and that it can be extended to CC stretching frequencies and CC bond lengths. Also, it is possible to predict CH or CC dissociation energies using the corresponding AIM stretching frequencies.
For further reference, see:
- 186New Developments in the Analysis of Vibrational Spectra: On the Use of Adiabatic Internal Vibrational Modes, D. Cremer, J. A. Larsson, and E. Kraka, Theoretical and Computational Chemistry, Volume 5, Theoretical Organic Chemistry, C. Parkanyi, Edt., Elsevier, Amsterdam, 1998, p.259-327.
- 195Theoretical Verification and Extension of the McKean Relationship between Bond Lengths and Stretching Frequencies, J.A. Larsson and D. Cremer, J. Mol.Struct., 485-486, 385-407 (1999)
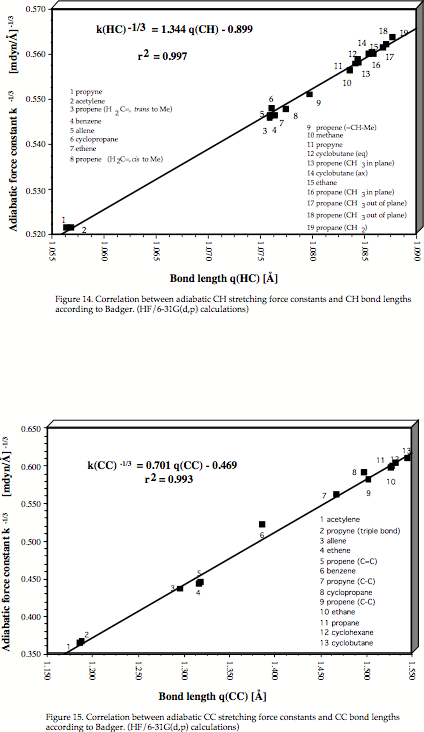
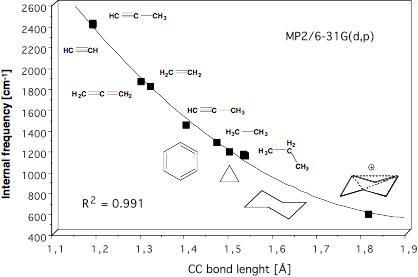
Figure 10. Determination of the C1C3 distance in the trishomotropenylium cation with the help of a quadratic correlation between adiabatic CC stretching frequencies and CC equilibrium bond lengths both calculated at the MP2/6-31G(d,p) level of theory [42].
3. Correlation of the spectra of isotopomers
There are four different quantities of a molecule, which have a direct influence on its vibrational spectra, namely the number N of the atoms constituting the molecule, the molecular symmetry X, the masses m_i of the atoms (collected in the mass matrix M), and the electronic structure of the molecule as reflected by its force constant matrix K. Changes in one or more of these quantities leads to changes in the vibrational spectra. If experimentalists are able to measure the changes in the vibrational spectra, one can draw conclusions with regard to the changes in the molecular quantities influencing the vibrational spectra. This may sound trivial, however already a change in N represents a serious problem of correlating a smaller with a larger number of vibrational modes in such a way that changes in the electronic structure accompanying a change in the number of atoms are clearly identified.
If one would be able to exactly identify changes in the vibrational spectra, which accompany a change in either N, M, X or K, one would be able to extract valuable information from infrared or Raman spectra. Hence the automated correlation of the vibrational spectra of related species is an important goal of vibrational spectroscopy. This goal can be split up into partial problems by varying one of the four quantities influencing a vibrational spectrum and keeping all other fixed.
- Changes in K while keeping N, X, and M fixed: correlation of the vibrational spectra along a reaction path;
- Changes in K and X while keeping N and M fixed: correlation of the vibrational spectra of isomers and conformers;
- Changes in M and X while keeping N and K fixed: correlation of isotopomer spectra;
- Changes in K, M, and X while keeping N fixed: correlation of the vibrational spectra of valence isomers;
- Changes in N, K, M, and X: correlation of the vibrational spectra of different compounds.
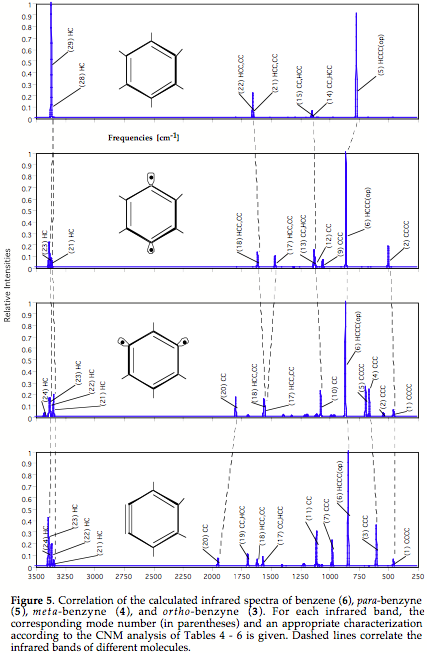
In the latter case, there must be at least some structural or chemical relationship between the compounds considered to make a correlation of the vibrational spectra meaningful (typical example: parent and substituted compound such as benzene and toluene).
We have recently worked on problem 1) because it is related to the description of a chemical reaction with the help of the reaction path Hamiltonian and the unified reaction valley approach. The reaction complex of a chemical reaction keeps its symmetry along the reaction path and can only change it at a stationary point (McIver-Stanton rules). The problem of correlating the generalized normal modes along the reaction path we solved with a diabatic ordering of the vibrational modes (DMOD), which was used already in a number of reaction mechanism studies.
Problem 2 is closely related to problem 1: For each pair of conformers, one can identify a reaction path in conformational space and consider the correlation problem as the problem of monitoring the vibrational modes between reactant (conformer 1) and product (conformer 2). Special consideration has to be taken concerning the change in symmetry at the stationary points. A similar approach could be taken in the case of configurational isomers although this might lead to unusual reaction paths with high barriers. Clearly, this way is feasible, however leads to a large number of costly calculations whereas the additional gain in information is not needed in the normal case. Hence, problem 2 might be considered to be solved in a new way including a change in mass. For example a cis- and a trans-isomer such as cis- and trans-difluoroethene, can be related by growing at a position of a H atom the mass of a F atom and shrinking at the position of a F atom the mass to a H atom. If these changes are accompanied by appropriate changes in the force constant matrix K it is possible to correlate the vibrational spectra of configurational isomers. However to solve this task in an appropriate way we consider first the problem of correlating the vibrational spectra of isotopomers (task 3).
In the literature there have been simple recipes to estimate the isotope shifts of vibrational frequencies and correlate the vibrational spectra of isotopomers on the basis of these estimates. Best known are the Teller-Redlich product rules or the various sum rules for the vibrational frequencies of isotopomers. Teller and later Wilson described perturbational approaches, which use the fact that, apart from the substitution of hydrogen by deuterium, the mass change in a molecule caused by isotope substitution is normally rather small and can be considered as a mass perturbation to the unperturbed vibrational problem. Zivkovic has suggested a more general perturbation method to predict isotope shifts for vibrational frequencies. This method does no longer require that the mass changes are small and therefore, it is no longer limited to just a few favorable cases as the Teller-Wilson methods were.
Since we wanted to approach this problem in a general way leading also to simple solutions for problems 2) and 4) and, then, to an automated correlation of the vibrational spectra of any pair of compounds with a common chemical basis (all compounds with the same number of atoms and the same symmetry, parent compound and its derivatives, configurational and conformational isomers, etc.), we disregarded the known ways of predicting isotope shifts. Instead, we solved problem 3) independent of the change in mass or symmetry just assuming that the change in the force field (potential energy function) is negligible, which is certainly true for the harmonic approximation generally used to calculate vibrational spectra with quantum chemical methods. For this purpose, we partitioned the problem into two sub-problems:
3a) Changes in M while keeping N, X, and K fixed: correlation of the vibrational spectra of isotopomers of the same symmetry;
3b) Changes in M and X while keeping N and K fixed: general correlation of the vibrational spectra of isotopomers.
For the purpose of solving these problems, we defined a mass reaction path and a mass reaction path hamiltonian. With the help of these definitions, we were able to apply the DMOD approach to correlate the vibrational spectra of isotopomers. Using the concept of a mass reaction path an algorithm was developed that leads to the correct correlation of the vibrational modes of two isotopomers. The mass reaction path was defined by weighted incremental changes of the masses in a molecule which, successively applied, convert the "mass reactant" into the "mass product". Overlap criteria were used to correlate the vibrational modes in the correct way between two path points considering both changes in symmetry, avoided crossings and rotations among degenerate modes. The new algorithm was formulated in a way that it can be extended to the correlation of the vibrational spectra of structurally related molecules.
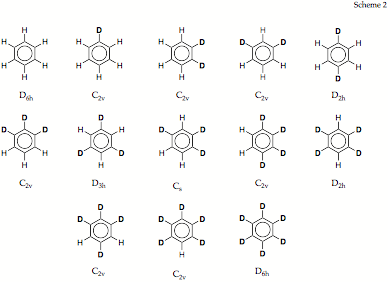
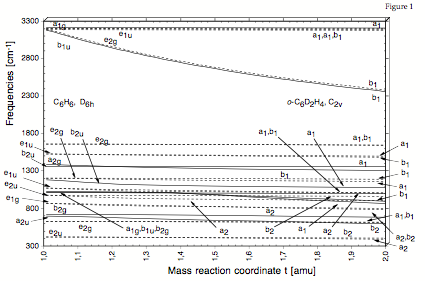
Figure 1. Correlation of the vibrational frequencies of benzene, C6H6, and 1,2-dideutero-benzene, C6D2H4, using a mass reaction path and the DMOD algorithm.
4. Automation of the Analysis of Vibrational Spectra
The analysis of vibrational spectra heavily relies on group characteristic vibrational frequencies, which are used to describe the structure of a given molecule. Such an approach is contradictory in itself as the normal modes of a molecule are delocalized modes, which are not limited to a particular fragment but extend by coupling into other parts of the molecule. Therefore, the normal mode analysis used in vibrational spectroscopy is an insufficient starting basis to deduce from measured spectra geometry and conformation of a molecule. We developed the adiabatic vibrational modes and the characterization of normal modes concept, which in combination provide an excellent basis for the automation of the analysis of vibrational spectra.
The project is planned to proceed in three steps:
- Development of an automated analysis of isotopomer spectra (changes in the masses of the atoms of a molecule). Work will be based on the mass analogue of a reaction path Hamiltonian.
- Development of an automated analysis of isomer spectra (changes in the force field and the symmetry of a molecule). This requires symmetry correlation or, alternatively the use of catastrophe theory.
- Development of an automated analysis of the spectra of valence isomers (changes in the force field, the symmetry, and the masses of the atoms of a molecule).
Techniques needed for 1) and 2) have to be combined in this case. - If problems 1) - 3) are solved it should be in principal possible to correlate the vibrational spectra of chemically related molecules such as benzene and toluene, where the change in the number of atoms corresponds to an additional problem, which however can be again handled by using catastrophe theory.
An automated analysis and correlation of vibrational spectra would be of high value for both experimentalists and theoretician, in particular as the use of the adiabatic modes, which can be determined for both calculated and experimental spectra, leads to detailed information on chemical bonding and the geometry of the molecules investigated.