van der Waals Complexes

VIII) Description of van der Waals Complexes

Description of Van der Waals Complexes by Theoretical Means
Description of van der Waals Complexes and Loosely Bound Transition States with DFT Methods
SAPT and Electron Density Investigation of Argon-Arene and Argon-Alkene van der Waals complexes
The Microwave Spectrum, Ab Initio Analysis, and Structure of the Fluorobenzene-Hydrogen Chloride Complex

1. Description of Van der Waals Complexes by Theoretical Means

(Project leader: Elfi Kraka)

Investigations of van der Waals complexes are one of the challenges of our time since they lead to a first understanding of the forces that act between molecules in bulk matter, of the interactions between a solute and a solvent or those between adsorbed molecules and a surface. Although one knows that the forces acting in van der Waals complexes are of the electrostatic, induction, exchange repulsion, and dispersion type, their composition in dependence of the electronic structure of the complex partners and their role in the determination of complex stability, geometry and other properties emerges only slowly out of literally hundreds of investigations.

Originally our search focused on argon complexes with aromatic molecules since these complexes provide excellent examples to investigate the forces that determine complex geometry and complex stability. In a joint venture with the microwave spectroscopy group of H. Dreizler (University of Kiel, Germany), we studied the properties of Ar complexes with benzene, pyridine, oxazole, isoxazole, thiophene, etc. This research was based on Coupled Cluster (CC) and perturbation theory calculations and has led to a new way of analyzing and understanding the forces acting in van der Waals complexes. Essential for this analysis is the calculation of the electron density distribution of complex and pro-complex along the lines described previously (see, for example, "Chemical Implication of Local Features of the Electron Density Distribution", E. Kraka, D. Cremer, in "Theoretical Models of Chemical Bonding", Z.B. Maksic, Edt., Volume 2, The Concept of the Chemical Bond, Springer Verlag, Heidelberg, 1990, p. 453.). For this purpose the difference electron density distribution Dr(r) as well as the difference Laplace concentration D{Ñ2r(r)} are evaluated and investigated.

Previous attempts to understand the electronic nature of van der Waals complexes by investigating its electron density distribution have failed for various reasons that have become obvious in our research. A number of prerequisites have to be fulfilled to carry out such an analysis.

The difference electron density distribution of a van der Waals complex is mostly in the range 10-4 to 10-8 a.u. and, therefore, its analysis requires high-precision calculation (convergence criterion for the elements of the density matrix at least 10-9).
The density analysis has to be based on MPn (n=4) or Coupled Cluster response densities because only at this level of theory a van der Waals complex is reasonably well described.
The equilibrium geometry of the complex has to be correctly evaluated, which in view of the flatness of the potential energy surface in the vicinity of the global minimum requires high precision.
Most important, all calculations (geometry optimization, property calculations, analysis of the electron density) have to be carried out for BSSE corrected wave functions. Originally, this had not been considered, which led to many misinterpretations of ab initio electron density distributions.

By fulfilling requirements 1) to 4) we showed that e.g. the properties of Ar-van der Waals complexes are dominated by two factors, namely a) the exchange repulsion forces, which preferentially determine the equilibrium geometry of the complex, and b) the dispersion forces, which preferentially determine the complex stability. With the help of the electron density distribution and its Laplace concentration exchange repulsion forces can be visualized. They encase the molecule like a cloud, where bays and pockets correspond to places with smaller exchange repulsion forces. A partner molecule or atom is looking for these bays and pockets to approach the molecule as close as possible to maximize induction and dispersion forces, which in the case of argon van der Waals complex are responsible for the complex stability. By knowing the bays and pockets of the exchange repulsion forces, the complex geometry can be predicted.

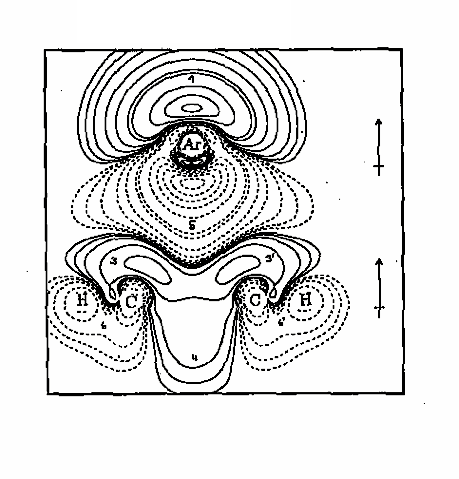
Figure 1. The difference electron density distribution of the argon-benzene complex is shown in form of a contour line diagram taken in the plane that cuts through two CH groups and the center of the benzene ring as well as through the Ar atom. The Ar atom approaches the center of the benzene ring from above since over the ring center exchange repulsion is lowest (a "bay" indicated by the solid contour lines which correspond to an increase of electron density in the complex relative to the pro-complex). In this way, the complex stability adopts a maximum.

2. Description of van der Waals Complexes and Loosely Bound Transition States with DFT Methods

Gradient-corrected density functional theory (DFT) methods and especially the so-called hybrid functional methods have successfully been applied to many chemical problems, however they severely fail in the case of van der Waals complexes and loosely bound transition states. Van der Waals interactions result from density fluctuations in regions significantly separated in space. These are not properly described by standard DFT methods being based on the uniform electron gas model even when corrected by the gradient of the electron density. One way to correct for this deficiency is to add a term to the DFT energy expression that will be constructed from the densities of the complex-partners, namely r(partner 1) r(partner 2)/R6, and has the well-known R-6 dependence on the distance R between the complex partners.

We developed a generally applicable DFT method for van der Waals complexes and loosely bound transition states and systematically checked a variety of possible corrections terms including other long-range corrections. Such a DFT method is needed because DFT provides a reasonable compromise between cost and accuracy in the case of larger reaction systems. Apart from this, a large-scale investigation of van der Waals complexes would become possible.

Much research has focused on the investigation of van der Waals complexes. This is amply documented in a multitude of research papers and national research funding plans. Insights in the properties of van der Waals complexes in the gas phase transcend into condensed phases in so far as they lead to first understanding of the forces that act between molecules in bulk matter, of the van der Waals interactions between a solute and a solvent or those between adsorbed molecules and a surface. Therefore, development of a reliable DFT method for calculating van der Waals complexes increases chances for investigating larger reaction systems.

3. SAPT and Electron Density Investigation of Argon-Arene and Argon-Alkene van der Waals complexes

A large number of experimental and theoretical investigations in the past focused on van der Waals hetero clusters consisting of rare gas atoms bound to mono- or poly-cyclic aromatic molecules. These complexes are excellent models for understanding the structural and dynamical aspects of solvation processes, condensed-phase properties in liquids and solids, and cluster dynamics. Both experimental and theoretical investigations probed the structures, binding energies, and intermolecular vibrational frequencies of Ar-arene and Ar-alkene complexes. However, none of these theoretical studies has examined the interplay of attractive and repulsive forces in governing the interactions of the inert rare gas atom and p electron containing aromatic or olefinic systems.

While qualitative attempts have been made to address some of these issues, there has been no quantitative appraisal of the magnitude of the various attractive and repulsive forces and their roles in the formation of these complexes. One of the crucial factors, which impede quantitative investigations, is the high level of theory needed to accurately describe the interaction of an inert rare gas and the diffuse p electron clouds of the p system. This is because the major attractive component of these interactions is predominantly dispersive in nature, which can only be adequately described at the Coupled Cluster level of theory using at least a VTZ+2P basis set. Attractive forces are mainly comprised of electrostatic, dispersive and inductive interactions whereas the repulsive forces are mostly due to exchange repulsions. Each of these components has a different physical origin, magnitude and directionality. Dispersion forces result from the mutual polarization of the electron densities of the two interacting monomers while repulsive forces are caused by the Pauli exclusion principle, which prevents the electrons of one monomer from penetrating into the occupied space of the other monomer. This exchange repulsion increases with increasing overlap and is always destabilizing.

We performed perturbational calculations utilizing Symmetry Adapted Perturbation Theory (SAPT) to decompose the binding energy of a van der Waals complex into individual interaction energy components. SAPT provides a rigorous quantitative description of the intermolecular forces and also enables one to identify the physically meaningful terms originating from classical theories of intermolecular forces. Unlike most other decomposition procedures, SAPT allows for a natural description of the interaction energy in the form the following terms:

E{elst}⁽¹⁾
electrostatic energy of the monomers with the unperturbed electron distribution,
E{exch}⁽¹⁾
electrostatic energy of the monomers with the unperturbed electron distribution,
E{ind}⁽²⁾
the second-order energy gain coming from the induction interaction,
E{exch-ind}⁽²⁾
the repulsion change due to the electronic cloud deformation,
E{disp}⁽²⁾
the second-order dispersion energy,
E{exch-disp}⁽²⁾
the second-order correction for a coupling between the exchange repulsion and the dispersion interaction, and
d{int}^HF
including the higher order induction and exchange corrections.

We carried out first conventional supermolecular (SM) calculations to obtain the optimized geometries, binding energies and vibrational frequencies of Ar-benzene, substituted Ar-benzene, and Ar-alkene complexes. Basis set superposition error (BSSE) corrections for the SM calculations were determined using the counterpoise (CP) method of Boys and Bernardi. Since BSSEs can also lead to changes in the complex geometries and densities, we performed also CP corrected geometry optimizations and calculated CP corrected electron densities. We used second order Møller-Plesset perturbation theory employing an augmented VDZP basis set, for which we could show that it leads to reasonable results due to a fortuitous cancellation of correlation and basis set errors. In addition, we carried out calculations with Dunning's aug-cc-pVTZ basis set. The energy decomposition analysis was complemented by electron density analysis, which helped to predict the most likely approach direction of the two monomers and explain the most stable complex geometry.

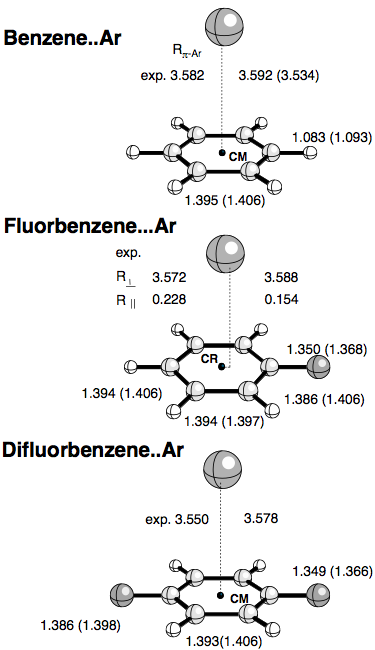
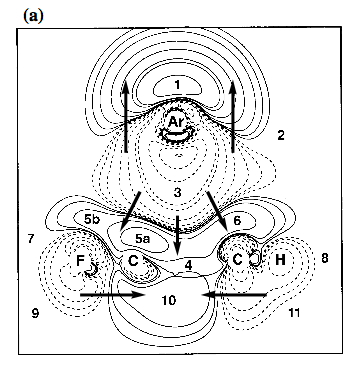
Figure 3. Contour line diagram of the MP2 difference electron density distribution of fluorobenzene-argon calculated with a [7s4p2d1f/4s3p1d/3s1p] basis at optimized geometry. Reference plane is the plane perpendicular to the benzene ring that contains Ar and the C1-F / C4-H bonds. Contour lines range from 2 10^-6 to 2 10^-1 [e/Bohr³]. Solid lines correspond to an increase of electron density upon complex formation, dashed lines to a decrease. Regions of increase and decrease of electron density are marked by small numbers. Arrows give the direction of charge polarization.

4. The Microwave Spectrum, Ab Initio Analysis, and Structure of the Fluorobenzene-Hydrogen Chloride Complex

The fluorobenzene-hydrogen chloride π-hydrogen bonded complex was studied by high resolution microwave spectroscopy and ab initio calculations. Rotational spectra of the C₆H₅F-H³⁵Cl, C₆H₅F-H³⁷Cl and C₆D₅F-H³⁵Cl isotopomers were assigned using pulsed molecular beam techniques in a Fourier-transform microwave spectrometer. The spectra are consistent with the HCl above the fluorobenzene ring near the ring center similar to the benzene-HCl prototype dimer. The inertial data is not sensitive to the precise location of the hydrogen in the HCl. Interpretation of the chlorine quadrupole coupling constant, usually employed to orient the HCl in complexes, is also ambiguous due to sign ambiguities and large amplitude vibrational effects. Ab initio calculations (MP2/6-311++G(2df,2pd) + BSSE corrections) indicate that the position of the HCl is driven by electrostatic interactions with the π electrons of the benzene ring. HCl is shifted by 0.16 Å from the center of the ring toward the para-C atom where the p-density is significantly higher. In the equilibrium form, HCl is tilted by d = 14° from perpendicular to the ring with the hydrogen end toward the para-C atom. The H atom can perform an internal rotation or at least a half-circular libration (barriers smaller than 100 cm-1), in which the inclination angle d varies only slightly. An average d value of 0.7° can be estimated in reasonable agreement with the measured vibrationally averaged d of 3.8°. The complex binding energy DE calculated at the CCSD(T)/6-311++G(2df,2pd) + CP(BSSE) level of theory is 2.8 kcal/mol suggesting a lower DE values for benzene-HCl than previously reported. Fluorobenzene-HCl possesses some charge transfer character, however just 5.5 melectron are transfered from the benzene ring to HCl. In view of this, p-H bonding in fluorobenzene-HCl is predominantly electrostatic rather than covalent in character contrary to claims made in connection with benzene-HCl.

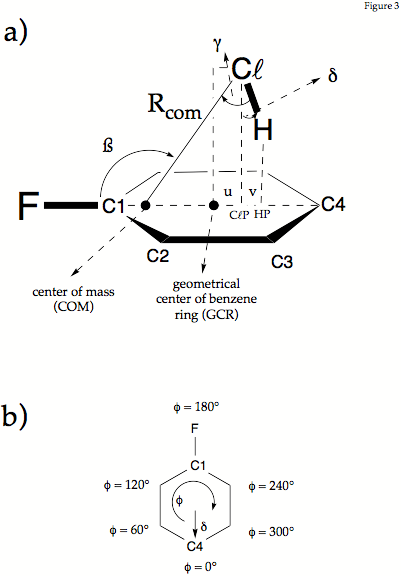
Figure 2. Definition of the geometrical parameters used in the description of fluorobenzene-HCl. a) Distance R_com connects the Cl atom with the center of mass. The projection of HCl into the plane of the ring are given by the points HP and ClP where R(Cl,ClP) and R(H,HP) are the projection lengths. The Cl and the H atom are shifted by lengths b and b+c from the GCR (geometrical center of the ring) toward C4. The angle ß is the angle between the CF bond axis and R_com.The angle g is the angle between R_com and the ClH bond axis. Angle d measures the deviation of the ClH bond axis from the perpendicular direction given by Cl,ClP. In the mirror plane of the complex d is given by d = g+90-ß. Note that g can adopt positive and negative values while d is always positive. - b) The internal rotation of the HCl molecule is described by the phase angle f and the angle d, that takes the role of a radial parameter. Angle d varries for f = 0 to 360°.

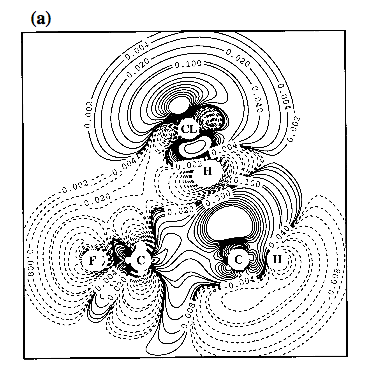
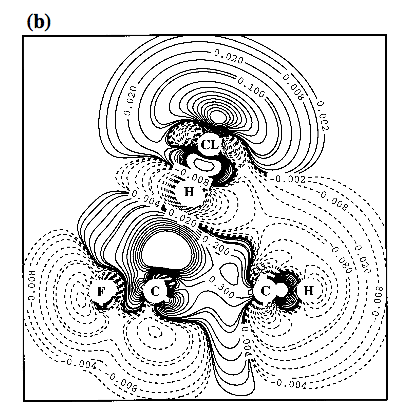
Figure 4. Contour line diagram of the MP2 difference electron density distribution of fluorobenzene-HCl for two positions of HCl: a) f = 0° and d = 14° (g = 24°); b) f = 180° and d = 14° (g = -4°). - The Cl atom is centered over the GCR for reasons of comparison with Figure 3. Reference plane is the plane perpendicular to the benzene ring that contains HCl and the C1-F / C4-H bonds. Contour lines range from 2 10^-6 to 2 10^-1 [e/Bohr³]. Solid lines correspond to an increase of electron density upon complex formation, dashed lines to a decrease.

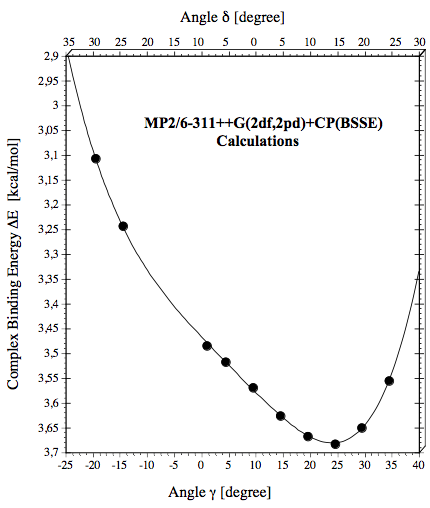
Figure 5. The complex binding energy calculated at the MP2/6-311++G(2df,2pd) + CP(BSSE) level of theory is given as a function of the inclination angles d (top scale)and g (bottom scale).

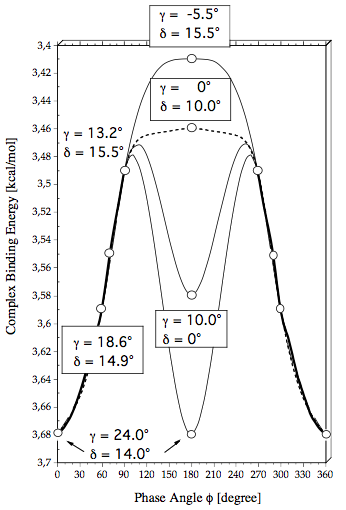
Figure 6. The complex binding energy calculated at the MP2/6-311++G(2df,2pd) + CP(BSSE) level of theory is given as a function of the phase angle f. For selected points the optimized values of inclination angles g and d are given. The bold line indicates the f-region of a large amplitude libration while the thin and dashed lines indicate possible rotation paths characterized by fixed values of g and d.