V) NMR Spectroscopy and Analysis of NMR Parameters
VI) Development and Application of Relativistic Methods
1. Development and Application of a Program for NMR Coupling Constants based on Density Functional Theory
In 2000, we developed the first DFT program that fully calculates NMR spin,spin coupling constants (SSCCs) within the Coupled Perturbed DFT (CPDFT) approach. Similar developments dating to years before 2000 can be found in the literature, however they were based on the programming of just one or three of the four Ramsey terms that determine the value of the SSCC, namely the Fermi contact (FC), the spin-dipole (SD), the paramagnetic spin-orbit (PSO), and the diamagnetic spin-orbit (DSO) term. None of the previous developments succeeded in setting up the SD term and the argument used in this connection was that this term is rather small. This however is only true for hydrocarbons, but as soon as hetero atoms with electron lone pairs are involved, this argument does no longer hold as we could demonstrate for NX, OX, FX coupling constants (X = H, C, N, O, F).
We tested local, nonlocal (GGA), and hybrid functionals, where the latter were optimized for the particular purpose of calculating SSCCs. It turned out that a GGA functional is absolutely necessary to obtain reliable values, however performance can be improved by using a suitable hybrid functional. We designed a hybrid functional that can reproduce experimental SSCC values in a reliable way reaching almost Coupled Cluster accuracy.
In addition to the CPDFT method Sum-over-states density functional perturbation theory (SOS-DFPT) and Coupled perturbed Hartree-Fock (CPHF) programs were set up to have also methods available, which were used in the past to calculate SSCC values.
SSCCs were calculated with CPDFT, EOM-CCSD, CCSD, CPHF, and SOS-DFPT where CCSD was used for accurate descriptions and CPDFT for large scale calculations of indirect SSCCs.
For typical hydrocarbons and other typical first row molecules containing hetero atoms such as N, O, F, we investigated the electronic mechanism, which determines the sign and the magnitude of the SSCC. One finds in the literature similar studies, however they normally concentrate just on the FC term, which dominates often but not always the value of the SSCC. We could demonstrate under which conditions SD and PSO term become also important.
2. Description of Pseudorotating Molecules with the help of NMR
For the pseudorotating cyclopentane molecule, we determined the dependence of the SSCC on the conformational changes of the molecule during pseudorotation using both the CPDFT and EOM-CCSD methods. These calculations are the basis for studies of biochemically interesting molecules because they answered the following questions: a) Is it possible to use NMR spectroscopy in connection with quantum chemical calculations to accurately determine the conformation and geometry of biochemically interesting molecules in solution? b) Can one generalize for this purpose Karplus type descriptions such as:
nJ(t) = A cos 2t - B cos t + C. (1)
(n = 3 gives the number of bonds connecting the coupling nuclei X and Y; coefficients A, B, C determine the dependence of 3J(t) on the torsional angle t)?
Clearly, in the case of a rapidly rotating (pseudorotating) molecule, experiment can only provide average values and, then it is the question whether theory is able to unravel the complete information hidden in the experimental values.
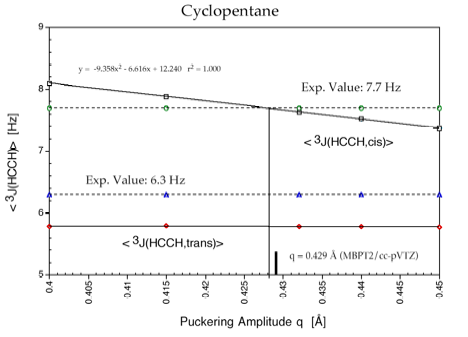
Cyclopentane is rapidly pseudorotating and only one cis 3J(H,H) and one trans 3J(H,H) coupling constant can be measured. We determined the pseudorotation potential of cyclopentane by MP2/cc-pVQZ calculations and, then, calculated all H,H, CH, CC coupling constants in dependence on the pseudorotation angle. It turned out that only a subset of four coupling constants shows a clear dependence on the pseudorotation angle and can, therefore, be used for determining conformational features. The second important result was that for all coupling constants Karplus type equations (1) can be set up, however their accuracy is rather low and a given point on the Karplus curve does not uniquely define a particular conformation, e.g. its degree of non-planarity (puckering amplitude q) and its pseudorotation phase angle.
However, there are unique relationships between coupling constants, puckering amplitude and pseudorotation phase angle, which we were able to determine and which we can use to identify a particular conformation. Since cyclopentane is a freely pseudorotating molecule (barrier: 0.2 kcal/mol), we determined averaged coupling constants by considering the population of the conformational energy surface in a statistical way. Calculated and experimental H,H coupling constants differ by just 0.4 Hz, which is an excellent result considering that vibrational effects (not determined in our work) also play a role.
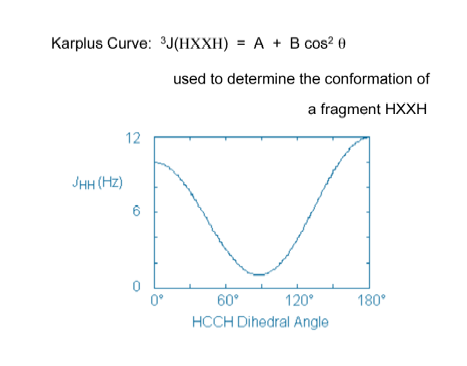
Figure A. Karplus curve for the ethane molecule. The vicinal proton-proton coupling constant is given as a function of the HCCH dihedral angle.
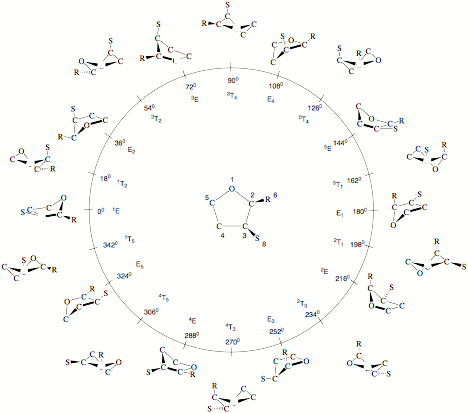
Figure 1. Pseudorotation itinerary (f = 0 to 360 degree) of tetrahydrofuran (THF) as indicated by the 10 E and ten T forms at f = (0 + k*360)/10 and f = (18 + k*360)/10 (k = 0,1,2,...,9). The pseudorotational space is spanned by q and f. At the center (q = 0), the planar ring is located. To distinguish different positions in the ring, symbols R, S are used for substituents. The numbering of the ring atoms defines the conformation at f= 0 degree and all subsequent conformations. Often the different E and T forms are identified according to a notation based on suitable reference planes taken from the E (atoms 2, 3, 4, 5) and the T form (atoms 1, 2, 5) of cyclopentane. Ring atoms, which lie above the reference plane are written as superscripts and precede the conformational symbol E or T, while ring atoms , which lie below the reference plane are written as subscripts and follow the symbol E and T. Since experimentalists often prefer this notation instead of using puckering coordinates, it is also given in Figure 1.
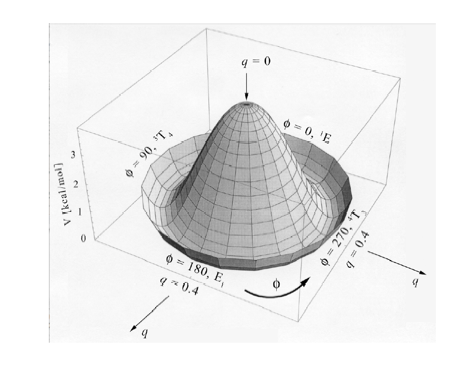
Figure 2. Perspective drawing of the three-dimensional conformational energy surface V(q, f) of THF. The planar form with q = 0 is located at the maximum. The direction of radial coordinate q and the angular coordinate f is indicated.
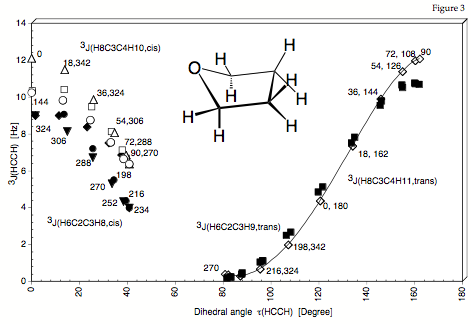
Figure 3. Dependence of the calculated SSCCs 3J(HCCH) of THF (H6C2C3H8 values are indicated by the following symbols: filled circles, open squares, filled diamonds, filled inverted triangles; H6C2C3H9: filled squares; H8C3C4H10: open triangles, open circles; H8C3C4H11: open diamonds) on the dihedral angle tau(HCCH) according to the traditional Karplus relationship. For each SSCC, the corresponding f value is also given (compare with Figure 1).
For the ring molecule it is not possible to expand the vicinal proton,proton spin-spin coupling constant accurately as a function of the appropriate dihedral angle. Values scatter for the low dihedral angles by 2 Hz and more. The dihedral angle does not provide a useful conformational parameter. Only the puckering coordinates describe correctly an unambiguously the ring conformation and therefore should be used for setting up the Karplus equation.
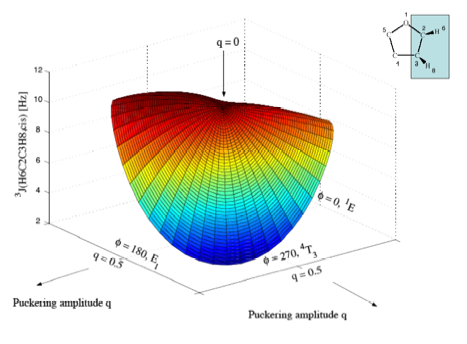
Figure 5a. Perspective drawing of the three-dimensional surface J(q, f) of SSCCs3J(H6C2C3H8,cis) of tetrahydrofuran. CPDFT/[6s,4p,1d/3s,1p] calculations. The explicit form of J(q, f) is given in Table 1. The direction of radial coordinate q and the angular coordinate f is indicated. Compare with Figure 1. Colors are given in the order of the rainbow spectrum from large to small J values changing every 2 Hz.
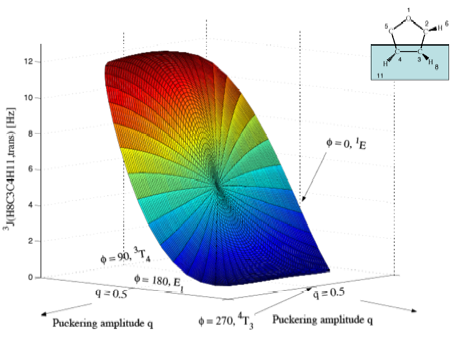
Figure 5b. Perspective drawing of the three-dimensional surface J(q, f) of 3J(H8C3C4H11,trans) of tetrahydrofuran. CPDFT/[6s,4p,1d/3s,1p] calculations. The explicit form of J(q, f) is given in Table 1. The direction of radial coordinate q and the angular coordinate f is indicated. Compare with Figure 1. The angle system has been rotated by 90 degree relative to those in a) to get a better viewing perspective. Puckering amplitude q = 0 is at the same position as in a), but hidden by the J-surface. Colors are given in the order of the rainbow spectrum from large to small J values changing every 2 Hz
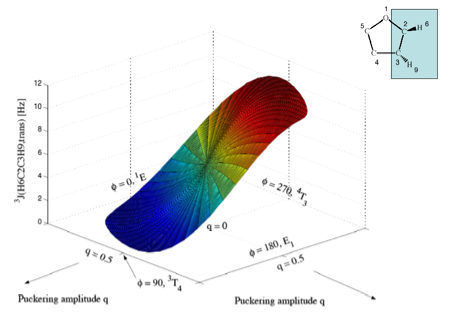
Figure 5c. Perspective drawing of the three-dimensional surface J(q, f) of SSCCs3J(H6C2C3H9,trans) of tetrahydrofuran. CPDFT/[6s,4p,1d/3s,1p] calculations. The explicit form of J(q, f) is given in Table 1. The direction of radial coordinate q and the angular coordinate f is indicated. Compare with Figure 1. Colors are given in the order of the rainbow spectrum from large to small J values changing every 2 Hz.
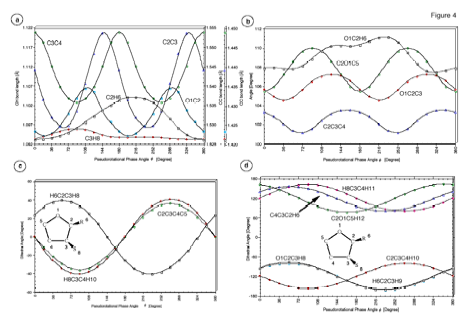
Figure 6. Dependence of the internal coordinates of THF on the pseudorotational phase angle f. (a) Bond lengths R(O1C2), R(C2C3), R(C3C4), R(C2H6) and R(C3H8). (b) Bond angles a(O1C2C3), a(C2C3C4), a(C2O1C5) and a(O1C2H6). (c) Dihedral angles t(C2C3C4C5), t(H8C3C4H10) and t(H6C2C3H8). (d) Dihedral angles t (O1C2C3H8), t(C2O1C5H12), t(C2C3C4H10), t(C4C3C2H6), t(H6C2C3H9), and t(H8C3C4H11). For the numbering of atoms, see Figure 1.
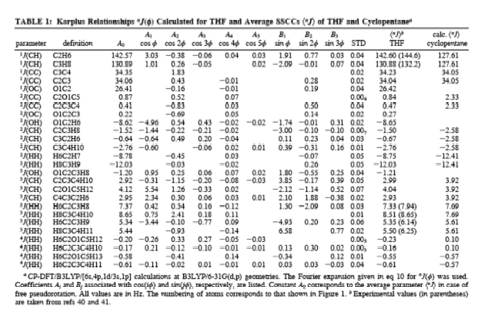
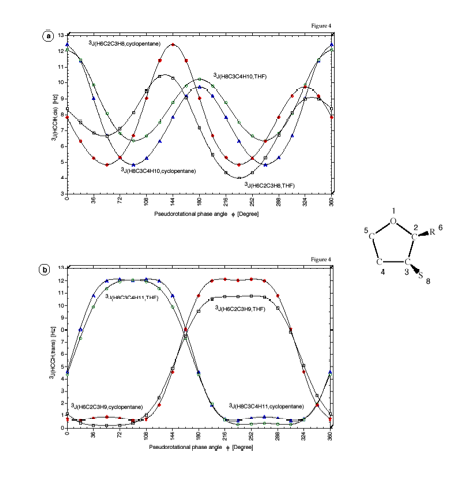
Figure 7. Dependence of the calculated SSCCs3J(HCCH) of cyclopentane and THF on the pseudorotational phase angle f (for the definition of J at f= 0 degree, see Figure 1). a) 3J(HCCH,cis), b) 3J(HCCH, trans). CPDFT/[6s,4p,1d/3s,1p] calculations.
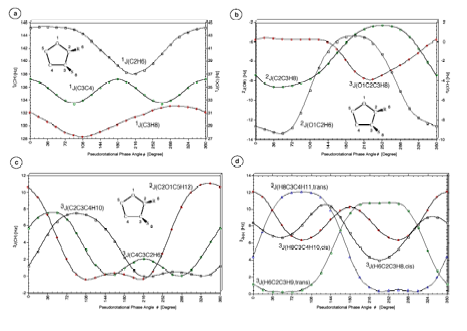
Figure 4. Calculated SSCCsnJ as a function of the pseudorotational phase angle f. (a) One-bond SSCCs1J(C2H6), 1J(C3C4) and 1J(C3H8). (b) 2J(O1C2H6), 2J(C2C3H8) and 3J(O1C2C3H8). (c) Vicinal SSCCs13C-1H SSCCs3J(C2O1C5H12), 3J(C2C3C4H10) and 3J(C4C3C2H6). (d) Vicinal SSCCs 1H-1H SSCCs3J(H6C2C3H8,cis), 3J(H6C2C3H9,trans), 3J(H8C3C4H10,cis), and 3J(H8C3C4H11,trans). For the numbering of atoms, see Figure 1. The coefficients of the Fourier expansions nJ(f) are listed in Table 1. All calculations at B3LYP/6-31G(d,p) geometries.