V) NMR Spectroscopy and Analysis of NMR Parameters
3. DORCO: Determining the Conformational Features of Pseudorotating Ring Molecules Utilizing Calculated and Measured NMR Spin-Spin Coupling Constants
A new method was developed to determine the most stable conformations of puckered rings by a comparison of measured and calculated SSCCs (DORCO: determination of ring conformations). The DORCO method extensively uses the ring puckering coordinates to express the properties of a pseudorotating puckered ring. In the case of NMR spin-spin coupling constants (SSCCs) J, this leads to an extension of the Karplus relationship to puckered rings. For five-membered rings with puckering coordinates q and f, the Karplus relationships adopt the form nJ(q, f) or nJ(f). It is shown that functions 3J(HCCH)(f) calculated with coupled perturbed density functional theory (CP-DFT) for a parent molecule can also be used for derivatives of the parent molecule and help to determine their conformational probability distribution function r(f). For this purpose, the DORCO procedure is developed to use functions nJ(f) of the parent molecule in connection with measured SSCCs of the substituted compound. DORCO was tested for tetrahydrofuran and two of its derivatives. The most stable conformations were determined by an accuracy of 4 % or better.
Theoretical Part
The different E and T forms shown of a 5-membered ring such THF are uniquely defined by the value of the pseudorotational angle f. Experimentalists often use an alternative notation of ring conformations based on suitable reference planes taken from the E (atoms 2, 3, 4, 5) and the T form (atoms 1, 2, 5) of cyclopentane. Ring atoms, which lie above the reference plane are written as superscripts and precede the conformational symbol E or T, whereas ring atoms, which lie below the reference plane are written as subscripts and follow the symbol E and T.
The use of the ring puckering coordinates has a number of advantages of which only two are mentioned here. a) The geometry of any puckered ring form with a given value of f (or q and f) can be optimized even if this form does not occupy a stationary point of the CES. This would not be possible when using Cartesian or internal coordinates.
b) Any property P(energy, internal coordinates, dipole moment, charge distribution, frequencies, magnetic properties) of a puckered ring undergoing pseudorotation can be described in terms of the puckering coordinates. For this purpose, P is expanded in a Fourier series of the pseudorotational phase angle f in the case of a five-membered ring (similar formulas apply to N-membered rings):


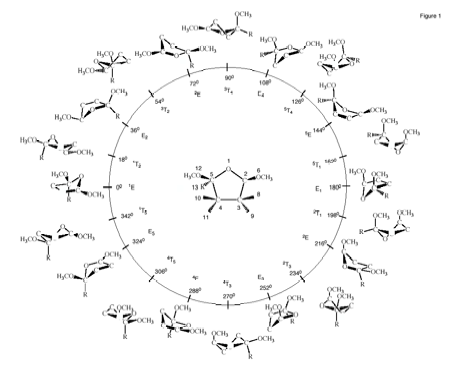
Figure 1. Pseudorotation itinerary (f = 0 right-arrow 360°) of cis-2,5-dimethoxy-tetrahydrofuran as indicated by the 10 envelope (E) and ten twist (T) forms at f = (0 + k*360)/10 and f = (18 + k*360)/10 (k = 0,1,2,...,9), respectively. At the center (q = 0), the planar ring is located. The position of the methoxy group in the case of trans-2,5-dimethoxy-tetrahydrofuran is indicated by the symbol R.
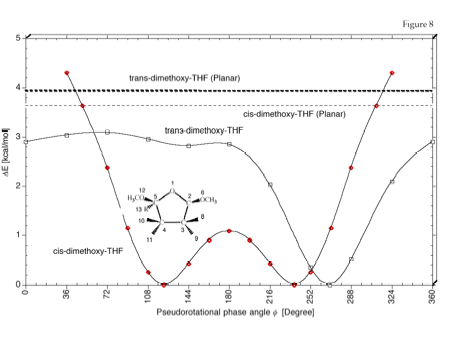
Figure 8. Pseudorotational potential of cis- and trans-2,5-dimethoxy-tetrahydrofuran. The inversion barriers are indicated by dashed lines. B3LYP/6-31G(d,p) calculations. Note that for the cis-derivative puckered forms collapse to the planar form for f = 0 ± Delta (Delta > 36 degree.
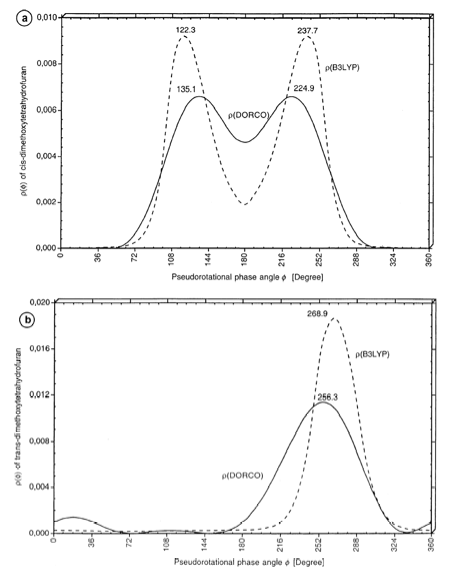
Figure 7. Conformational probability distribution function r(ƒ) as calculated by the DORCO method (solid line) and by B3LYP/6-31G(d,p) (dashed line). (a) cis-2,5-Dimethoxy-tetrahydrofuran and (b) trans-2,5-dimethoxy-tetrahydrofuran. The ƒ values of the energy minima ( = maxima of r(ƒ)) are given in each case. The most stable conformations in solution differ by a Delta f of 13 – 15 degree. Compare with Figure 8.
4. Investigation of Bonding in Intramolecular Donor-Acceptor Complexes by NMR
It is generally assumed that molecular structures do not vary much between the gas phase, solution or the solid state provided there are no significant chemical interactions between the target system and its environment. However, spectacular exceptions from this rule exist for molecules, which are easily deformed, e.g., by electrostatic interactions with the environment. Typical examples are intermolecular and intramolecular donor-acceptor (D-A) complexes where in particular the latter represent a class of molecules, which is highly interesting both for the theory of bonding and in connection with new materials (examples are silatranes). One has speculated that in D-Z-A molecules containing a B-C-N, B-N-N, Al-C-N, Al-N-N, Si-N-N, Ge-O-N or Sn-O-N unit the D and A atoms may be linked by a weak covalent bond that is switched on and off depending on the environment (construction of molecular switches). For example, various compounds of the type X3Si-O-NR2 have been synthesized and investigated. X-ray diffraction studies lead to a Si-O-N angle of just 79° whereas for the gas phase an angle larger than 100° is found.
We investigated bonding in D-Z-A molecules both in the gas and in condensed phases. The bridge between solution phase investigations and quantum chemistry investigations relevant for the gas phase was provided by NMR spectroscopy. NMR chemical shifts and NMR spin,spin coupling constants are highly sensitive to electronic structure changes and the accompanying geometric changes caused, e.g., by the surrounding medium (in a solvent or crystal state). A change in bonding when going from the gas to condensed phases is reflected for example by the indirect SSCC and by the changes in the FC, PSO, DSO and SP term. Our investigation comprised the following three steps:
- Combining experimental data with quantum chemical calculations the structures of various D-Z-A compounds were determined in different media (gas and condensed phases).
- Using continuum methods and our NMR/ab-initio/IGLO method we determined the structure of the target compounds in solution.
- The relationship between the magnetic properties of a molecule and its electronic structure were analyzed using the data material from a) and b). Especially, it was investigated how different modes of chemical bonding are reflected by NMR spin,spin coupling constants.
The project led to a generally applicable procedure that uses measured and calculated NMR parameters to determine the molecular geometry in solution (molecular geometries from NMR spectroscopy) and to describe features of the electronic structure with the help of magnetic properties.
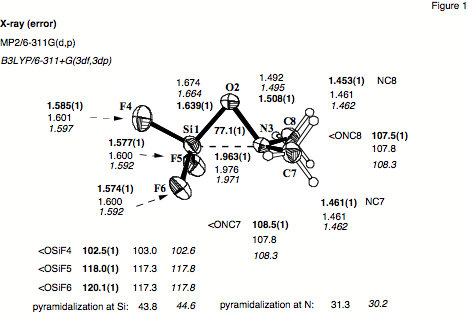
Figure 1. Solid state structure of F3SiONMe2 (1) as determined by low-temperature X-ray crystallography. The contents of the unit cell are shown at the 40% probability level.
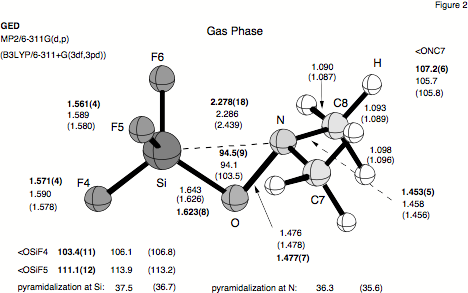
Figure 2. Atom numbering scheme and molecular geometry of F3SiONMe2 (1) as determined by gas-phase electron-diffraction (GED), MP2, and B3LYP.
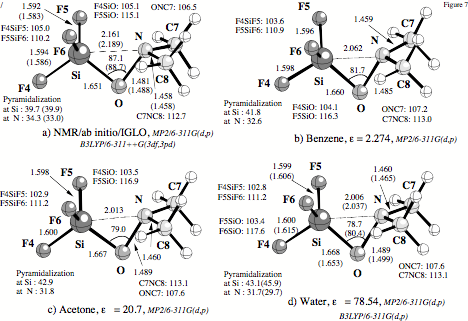
Figure 7. Geometry of 1 in solution as determined by (a) the NMR/ab initio/DFT-IGLO method using MP2/6-311G(d,p) [B3LYP/6-311++G(3df,3pd)] gas phase geometries (see text), (b) MP2/SCIPCM/6-311G(d,p) calculations for the dielectric constant of benzene, (c) MP2/SCIPCM/6-311G(d,p) calculations for the dielectric constant of acetone, and (d) B3LYP/SCIPCM/6-311G(d,p) calculations for the dielectric constant of water.
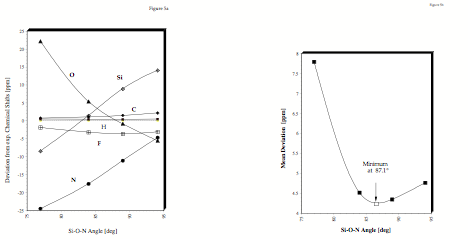
Figure 5. a) Difference between measured (C6D6 solution) and DFT-IGLO 1H, 13C, 15N, 17O, 19F, and 29Si NMR chemical shifts of 1 as a function of the Si×O×N angle. All values in ppm. b) Determination of the equilibrium value of the Si×O×N distance of 1 in C6D6 solution by NMR/ab-initio/DFT-IGLO calculations. The minimum of the mean deviation of all calculated NMR chemical shifts defines the equilibrium value of the Si×××N distance.
